

부동산 부양 정책, 담뱃세 인상과 같은 정책은 철저한 계산 아래 결정된다. 이러한 정책은 고전 경제학에 기반을 둔다. 고전 경제학의 ‘완전 시장’은 경제 주체가 매우 많아 개인의 행동이 시장에 영향을 미치지 못한다고 가정한다. 하지만 이는 구성원의 전략적 사고가 시장에 영향을 미치는 경우를 설명할 수 없다. 게임이론은 이를 보완하기 위해 도입된 이론으로, 경제 주체의 전략적 사고를 연구한다. 존 내쉬, 라인하르트 젤텐, 존 하사니가 게임이론으로 노벨상을 받으며 게임이론은 경제학의 주류로 부상했다.
게임이론은 여러 참여자가 주어진 정보를 기반으로 의사 결정을 하는 과정을 분석한 이론이다. 게임이론은 게임의 참여자가 점수를 얻으려는 것처럼 현실에서도 개인이 이익을 최대화하는 결정을 내린다고 가정한다. 현실은 게임보다 복잡하지만, 기초적인 유형의 게임인 ‘동시 게임’과 ‘순차 게임’을 조합해 표현할 수 있다. 동시 게임은 참여자들이 서로의 선택을 알지 못한 채 자신의 결정을 내리는 게임이며, 순차 게임은 앞서 결정한 사람들의 판단을 토대로 결정을 내릴 수 있는 게임이다.
각 참여자는 가능한 모든 수를 예측해 자신의 이익을 최대화할 수 있는 최선의 전략을 선택한다. 이때 모든 정보를 공유하면 참여자들은 타인의 결정을 예상할 수 있으며, 그 상황에서 자신의 이익을 최대화할 수 있는 전략을 세워 사용한다. 따라서 모든 정보가 공유된다면 참여자들이 선택할 최선의 전략과 게임의 결과는 정해져 있으며, 각자의 정해진 전략을 채택했을 때를 내쉬 균형이라고 부른다. 이익을 최대화하려는 사람들이 참여하는 게임에서 내쉬 균형과 다른 전략을 세운 참여자는 적은 보수를 받으므로, 그 게임의 결과는 항상 내쉬 균형이다.
블랙잭에서 이를 살펴보자. 블랙잭에서 딜러를 제외한 참여자는 패를 공개하므로, 각 참여자는 상대와 자신의 패에 대한 정보를 공유한다. 각 참여자는 그에 기반을 둬 패를 더 뽑았을 때와 뽑지 않았을 때의 손익을 계산해 의사를 결정한다. 하지만 자기 차례에 뽑을 패는 불확실한 정보다. 따라서 사람들은 이를 확률적으로 추측해 최선의 전략을 구하며, 각 참가자는 그 전략을 구사한다. 따라서 블랙잭에서도 내쉬 균형이 이뤄진다.
합리적인 결과를 가로막는 예측
두 죄수 A와 B가 심문을 받는 상황을 생각해보자. 두 죄수가 자백하지 않자 경찰이 다음과 같은 조건을 제시한다. “둘 중 한 명이 자백하면 그 사람은 무죄, 자백하지 않은 사람은 징역 25년으로 처리하겠다. 하지만 두 사람 모두 자백하면 각자 징역 5년, 모두 자백하지 않으면 각자 징역 1년을 선고하겠다” A와 B는 어떤 선택을 할까?
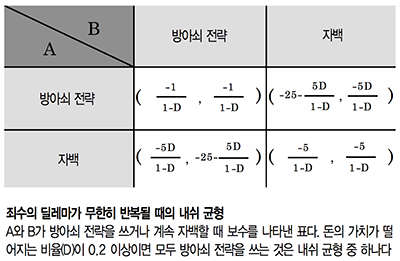
먼저 A의 처지에서 생각해보자. B가 자백을 했을 때, A가 자백을 하면 징역 5년을 선고 받고, A가 자백하지 않으면 징역 25년을 선고 받는다. 따라서 B가 자백을 하면 A는 자백하는 것이 최선이다. 그런데 B가 자백하지 않더라도, A가 자백을 하면 무죄가 되며 자백하지 않으면 징역 1년을 선고 받으므로 자백하는 것이 A에게 유리하다. 즉, B가 어떤 선택을 하든 A는 자백하는 것이 유리하다. B도 마찬가지므로 두 죄수는 자백을 하며, 이때가 내쉬 균형이다. 그런데 이는 두 죄수가 자백하지 않을 때보다 보수가 낮아 합리적이지 않다.
이처럼 죄수의 딜레마에서 개개인의 합리적인 참여자들이 높은 보수를 얻기 위해 만든 전략은 합리적이지 않다. 참여자는 우선 상대방이 특정 선택을 했다고 가정하고 그 뒤의 모든 결과를 예측하기 때문이다. 그러면 죄수의 딜레마에서는 상대방이 어떤 선택을 하든 ‘전체가 손해 볼 위험을 감수하고 자백을 한다’가 개인이 할 수 있는 최선의 선택이 된다. 그리고 모든 참여자들은 항상 이 전략을 선택하므로 비합리적인 결과 밖에 얻을 수 없다.
수학에서 실마리 찾아
사람의 사고를 합리적으로 예측하는 게임이론과 자연 현상을 탐구하는 자연과학은 문제를 해결하는 데 필요한 사고방식이 다르다. 하지만 두 학문에서 요구하는 사고방식이 다르다면, 서로의 난제를 다른 관점에서 해결할 수 있지 않을까? 게임이론의 유명한 예시인 ‘죄수의 딜레마’도 수학으로 해결할 수 있다.
학자들은 죄수의 딜레마를 해결하기 위해 무한 반복 게임을 고안했다. 무한 반복 게임에서는 시간에 따라 돈의 가치가 떨어지며 게임이 무한히 반복된다. 이때 돈의 가치가 떨어지는 비율이 일정하면 각 전략의 보수는 무한등비급수의 합으로 나타낼 수 있다. 죄수의 딜레마를 무한 반복 게임으로 가정하면, 상대방의 선택에 따라 어떤 선택을 해야 최선의 이익을 얻을지 일일이 예측하는 것은 불가능하다. 따라서 무한 반복 게임에서는 모든 선택의 순간에 보수를 일일히 비교하는 것이 아니라, 상대가 어떤 전략을 택하느냐에 따라 자신의 전략이 제공하는 보수의 합을 비교한다. ‘다른 참여자들이 합리적인 결과를 낼 수 있도록 협력하면 자신도 협력하고, 한 명이라도 협력하지 않는 행동을 보이면 그 후에는 절대 협력하지 않는다’라는 전략을 세워보자. 이 전략을 선택하면 개인은 가장 최선의 결과를 얻을 수 있다. 따라서 참여자는 이 전략을 채택해 모두가 항상 협조적으로 행동한다. 이 전략을 방아쇠 전략이라고 부르며, 자연과학에서 쓰이는 무한의 개념을 도입해 방아쇠 전략을 사용하면 죄수의 딜레마에서 합리적인 결과를 도출할 수 있다.
하지만 무한 반복 게임은 현실에 존재하지 않는 것으로, 실제 결과와 차이가 있을 수 있다. 액설로드는 ‘죄수의 딜레마 시합’을 통해 이를 증명했다. 그는 죄수의 딜레마를 200번 반복하는 컴퓨터 프로그램들을 서로 겨루게 했다. 그 결과 가장 높은 점수를 얻은 것은 ‘앞에서 상대가 협력했다면 협력하고, 그렇지 않으면 협력하지 않는다’라는 보복 전략을 구사한 프로그램이었다. 액설로드의 실험은 사람이 모든 경우의 수를 예측하는 것은 불가능하며, 항상 이론적인 전략을 구사하지 않는다는 점을 보여 게임이론에 몇 가지 문제를 제기했다.
데이터 전송 경로 찾는 게임이론
한편 게임이론을 공학에 적용한 사례도 있다. 게임이론의 한 분야인 메커니즘 디자인(Mechanism Design)을 살펴보자. 메커니즘 디자인이란 원하는 결과를 도출하는 게임을 설계하는 분야다. 이때 설계자는 참여자의 정보를 알지 못해 보수를 주고 정보를 제공 받는다. 그런데 참여자가 보수를 더 받기 위해 거짓 정보를 제공하면 게임은 설계자가 원하는 결과를 내지 못한다. 이를 막는 방법이 VCG 기법(Vickey Clarke Groves Mechanism)으로, 참여자의 최선의 전략이 사실을 말하는 것이 되도록 하는 방법이다.
학자들은 네트워크의 지연 시간을 줄이는 데 이를 사용했다. 네트워크에서 라우팅(Routing)은 전송 데이터를 전송하기 위한 경로를 찾는 과정이다. 라우팅할 때 참여자는 자신이 전송할 데이터의 양을 적절히 나눈다. 이때 개인이 자신의 비용을 최소화하기 위한 경로만을 찾으면 모두에게 최적화된 경로를 찾지 못해 전송 시간이 길어진다. 하지만 이때 VCG 기법을 라우팅에 활용하면 개인의 협조적인 행동을 유도할 수 있어 유용하다.










 홈
기획
홈
기획
